Discrete Fourier Transform - I
The Discrete Fourier Transform, takes in a sequence of N complex numbers \(x_0, x_1, \dots, x_{N-1}\) and converts them to another sequence, let’s say \(X_0, X_1, \dots, X_{N-1}\).
Inverse-DFT or IDFT, as the name implies, reverses the DFT. This whole process of conversion and de-conversion is achieved using the following equation pair.
DFT:
\[X_k = \frac{1}{\sqrt{N}} \sum_{n=0}^{N-1} x_n \cdot e^{-j 2 \pi k n / N}\]IDFT:
\[x_n = \frac{1}{\sqrt{N}} \sum_{k=0}^{N-1} X_k \cdot e^{j 2 \pi k n / N}\]Now this may look daunting. And this whole process certainly raised quite a few questions in my head the first time I saw it.
- Why are we doing it? (this post)
- Why complex exponentials? (part II)
- And most importantly, why do these pair of equations work? (part III)
Motivation
If you’re familiar with music you would know that different notes sound different because of pitch. Some sound shrill, some sound heavy. This difference is due to the frequency of the wave produced when you sing or play the note.
Each note is a vibration in the air, a to-and-fro motion. And the ones that vibrate faster sound shrill, the ones that vibrate slower sound bassy.
You can draw the wave, the to-and-fro intensity of air pressure vs time, on a graph using a sine-like wave. If the wave has small period, it has high-frequency, ie high pitch. And a larger period means low pitch.
\[\textrm{Pressure density} = s(t) = A \cdot \sin(2 \pi f t)\]Here \(f\) is the so called frequency of the wave. If \(f = 440Hz\), ie the to-and-fro motion happens \(440\) times in a second, we get the \(A4\) note.
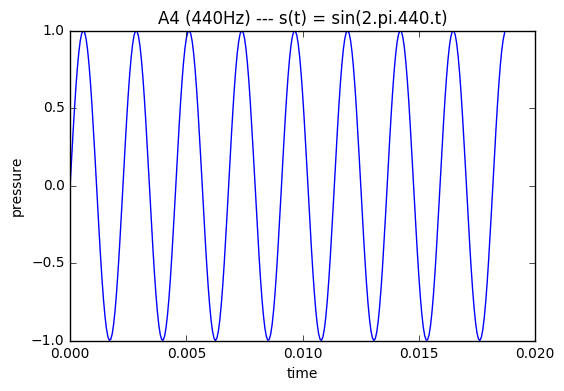
As you can see in the figure above, the wave covered 4.4 periods in 0.01 seconds.
A computer can’t record a continous wave of always-changing intensities, because there are uncountably infinite points on a continuous line. So it samples the pressure value thousands of times within a second. Like take a sample at \(1/1000\)th of a second, then at \(2/1000\)th and so on.
Doing this, you get a string of discrete numbers which represent the wave’s intensity at evenly spaced points of time. That is a sequence like:
\[x_0, x_1, \dots, x_{N-1}\]Here each \(x_i\) represents the \(i\)th sample. For \(i = 1001\), and sampling rate \(f_s = 1000\ Hz\) you can calculate the continuous time this sample corresponds to. It will be the amplitude of the wave at \(t = i/f_s = 1.001s\).
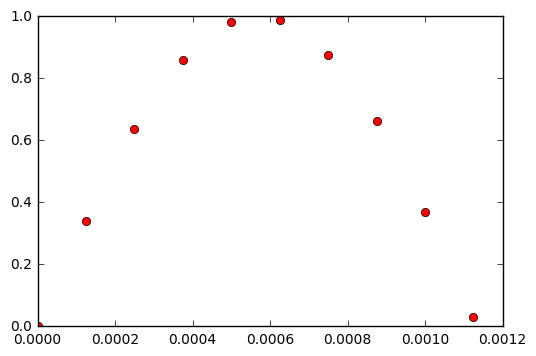
\[x_i = s\left(\frac{i}{f_s}\right)\]For example here are the first 10 samples of a 440Hz sine wave sampled at 8000 Hz:
X = [0, 0.33873792, 0.63742399, 0.86074203, 0.98228725, 0.98768834, 0.87630668, 0.66131187, 0.36812455, 0.03141076]
Now suppose you played two or three notes together, like in a chord. And you recorded that on a computer.
You’ve now got the sound signal of the chord as a list of numbers in your computer and you want to somehow figure out what notes were played in the chord, and with what intensites. How would you go about it?
If you played two notes of frequencies: \(f_1\) and \(f_2\). The continuous wave in the air would be something like:
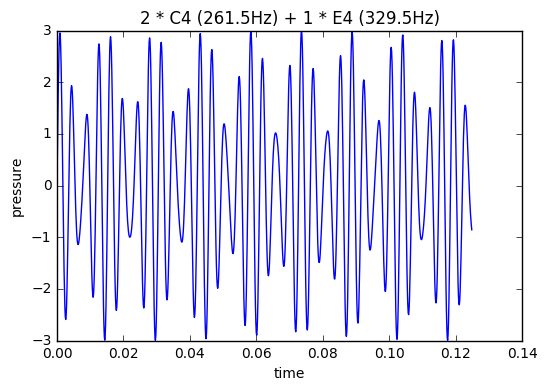
\[s(t) = A \cdot \sin(2 \pi f_1 t) + B \cdot \sin(2 \pi f_2 t)\]For example:
\(A = 2,\ f_1 = 261.5\ Hz\) (~ C4)
\(B = 1,\ f_2 = 329.5\ Hz\) (~ E4)
The string of numbers you’ll get will be given by:
\[x_n = A \cdot \sin\left(\frac{2 \pi f_1 n}{f_s}\right) + B \cdot \sin\left(\frac{2 \pi f_2 n}{f_s}\right)\]Here are the first few numbers from the C4-E4 chord (with \(f_s = 8000\ Hz\))
x = 0.0, 0.66379131852805939, 1.2933946833211722, 1.8564778507641972, 2.3243141125985418, 2.673326659067349, 2.886340129304954, 2.9534693906900813, 2.8725970774257692, 2.649415684497730, ...
Our aim here is to find a conversion method, which will take in this sequence of \(x_i\) and give us information about each frequency component in the wave.
We again encounter a problem though. The possible frequencies between suppose \(440Hz\) and \(441Hz\) are infinite, i.e. frequencies are also continuous. But our sad little computer needs to deal with non-infinite precision, i.e. discrete stuff.
Hence we reduce our problem from finding intensities of all possible frequencies, to just evenly spaced discrete frequencies. (NB: analytically, finding it for all frequencies is possible for a discrete-time sequence. It is called Discrete-Time Fourier Transform or DTFT)
We need to find a list of numbers \(X_0, X_1, \dots, X_{N-1}\), where each \(X_k\) corresponds to the contribution of a specific continous frequency \(f\) by the given formula:
\[f = \frac{k \cdot f_s}{N}\]It’s weird how \(f_s\) and \(N\) popped up here, isn’t it? I’ll hopefully cover it in another article, as it would be a major digression here. For now, think of \(k\) as just placeholders for equally spaced frequencies, and you can convert it back-and-forth using the formula given above.
Let’s apply this \(f\) to \(k\) conversion on our C4-E4 chord. The \(f_1 = 261.5\ Hz\) and \(f_2 = 329.5\) we picked, got sampled as (luckily integers):
\[k_1 = \frac{f_1 \cdot N}{f_s} = 261.5 * 16000 / 8000 = 523\] \[k_2 = \frac{f_2 \cdot N}{f_s} = 329.5 * 16000 / 8000 = 659\]Thus the chord wave in our computer can also be written as:
\[x_n = A \cdot \sin\left(\frac{2 \pi (523) n}{N}\right) + B \cdot \sin\left(\frac{2 \pi (659) n}{N}\right)\]Now we want to convert this sequence of \(x_n\) to a sequence of \(X_k\), such that:
\[X_{k_1=523} = 2, X_{k_2=659} = 1, \textrm{ rest } X_k = 0\]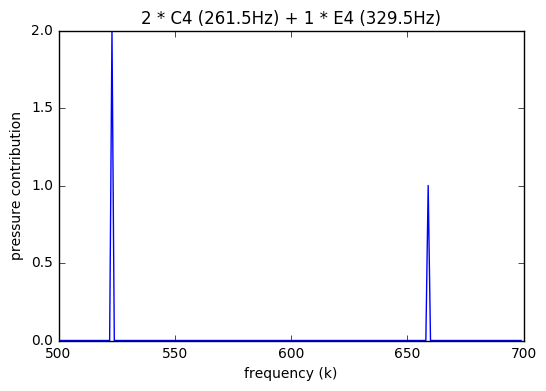
How to do this conversion? Answer of course is DFT, but I’ll cover it in Part II and III of this post.
To wrap up the motivation, consider this: In general if we already know all the \(X_k\) values for a sound wave, we can get the \(x_n\) samples of the audio simply by adding all the sine waves of the \(X_k\) frequencies:
\[x_n = \sum_{k=0}^{N-1} X_k \cdot \sin\left(\frac{2 \pi k n}{N}\right)\]You might notice how this looks eerily similar to the IDFT equation in the introduction. The only difference is the scary complex exponential instead of the sine, and the constant \(1/\sqrt{N}\) factor. So IDFT equation is just adding different discrete frequency contributions to form the \(x_n\) sequence.
If you’ve hung around till the end of this post without sleeping, congrats you almost understand IDFT. See you in the next post :)